From May to July 2020, I worked with Reinis Cirpons and Murray Whyte under the supervision of Prof. James Mitchell to extend the GAP Semigroups package. We worked mostly on free idempotent semigroups (free bands) and finitely presented idempotent semigroups.
Largely, semigroup theory is painfully abstract. Though it has applications in the theory of computation and other niche areas, I struggle to explain the basic concepts in a way which would excite my non-mathematical friends. So I was delighted to see, over the course of the summer, that through their definition via presentations, free bands are an exception to this rule. The idea of this blog post is to introduce the concept of the free band, and some basic big questions about it, in a way which requires very little mathematics. However, I hope that mathematicians will get some entertainment out of reading this too.
Pick some whole number $n$, and choose $n$ different letters or characters. I will keep an example in mind as I go through this post, and in this example, I will take $n=4$, and use the set of letters $\{a,b,c,d\}$. We call this set an alphabet, and we can create words out of this alphabet by taking finite sequences of letters: for example, $a$, $acc$, $abcdba$ and $aaaaaaada$ are all words.
The free band over this alphabet $\{a,b,c,d\}$ then consists of all possible words, but we will impose a rule which says that certain pairs of different letter sequences actually represent the same word. You could think of this as every word in English having multiple different spellings: the spellings may be distinct and may correspond to different sequences of characters, but they represent the same thing (for example, color and colour).
In the free band, the rule is that any chunk of letters can be doubled, and the resulting word is still equal to the original. Conversely, if a word contains two chunks of letters next to each other that are equal, we can cancel out one of the chunks to leave only one. So, by doubling the chunk $ab$, I get $ab=abab=ababab$, and this chunk can appear in bigger words: $cabd=cababd$. A chunk can also be a single letter: $bccd=bcd$.
Sometimes, it can take a lot of complicated steps to show that two words are in fact, through a sequence of duplications and cancellations, equal in the free band. For example, I claim that the following two words are equal: $abcacba = abcba$. Can you come up with a sequence of cancellations and duplications of chunks that will lead you from one to the other? If it’s better than my solution below, which took me a good hour and access to three papers to produce, please let me know in the comments!
The complexity of the proof I’ve just shown demonstrates that although the setup is simple to describe, complicated maths is needed to solve some of the harder problems. I’ll leave some references at the bottom of this post for anyone who is interested in finding out more.
For a mathematician, some natural questions that might arise when we define the free band are:
- How many actually different words are there in the free band? Can we get infinitely many distinct words, or is there only a finite number of possibilities?
- Given two sequences of letters, how can I tell whether they actually represent the same word?
- For very long words with lots of different letters, how long does it take to find the answer to 2.?
- If I know two words are equal, how can I infer the sequence of duplication/cancellation steps to get from one to the other?
All of these problems turn out to be nontrivial, and require quite a few pages of working. In fact, although a general method for question 4 exists, no-one has yet found a particularly efficient method.
Nevertheless, for some small values of $n$ (the size of the alphabet), you can work some of these solutions out by hand. For example, let’s take $n=2$ and choose the alphabet $\{a,b\}$. We’ll have a go at tackling question 1 in this setup. Recalling that you can cancel duplicates, try to write out as many words as you can that are all different (no sequence of steps could lead from one to the other), using only $a$ and $b$. How may do you find? The correct answer is below.
A general formula has been proven for the size of the free band on $n$ letters, and it turns out that the free band on $n$ letters is always finite, regardless of $n$ (though this is not necessarily obvious: for some technical further reading, note that the existence of this sequence precludes the use of straightforward arguments to show finiteness of the free band). For increasing values of alphabet size $n$, the free band size increases as follows:
| $n$ | Size of the free band on $n$ letters |
|---|---|
| $1$ | $1$ |
| $2$ | $6$ |
| $3$ | $159$ |
| $4$ | $332380$ |
| $5$ | $2751884514765$ |
Given this table, $n=2$ is the only case you’d really want to work out by hand. The numbers get large so quickly that there is basically no hope of storing a list of all the elements of the free band for more than 4 letters. Nevertheless, this answers question 1 to a pretty satisfactory extent.
We’ve covered some basics on question 1, and I’ll talk a bit about questions 2 and 3 now. I claimed earlier for no apparent reason that $abcacba = abcba$, and produced a rather complicated sequence of steps leading from one word to the other. However, some work by Green and Rees (two big names in semigroup theory) in the 1950s actually gives a pretty simple method to tell whether two words are equal, without having to write out a full sequence from one to the other. It involves some things called the initial and the terminal, and their associated marks.
Let’s pick a word in our example free band on $\{a,b,c,d\}$: say, $adcadbc$. We can now define the initial and the terminal of this word. To find the initial, we start reading the word from the left until we have seen every letter that appears in the word at least once. In this case, we would stop when we reach $adcadb$, since $b$ is the last letter to appear. Then the initial mark of $adcadbc$ is that last letter $b$, and the initial is everything up to the $b$, i.e. $adcad$ in this case. We do something analogous to find the terminal mark and the terminal of the word, reading from the right end instead and moving backwards until we have seen every letter at least once. You can check that the terminal mark is $a$ in this case, and the terminal is $dbc$.
Using this terminology, a standard result (that uses some complicated maths) is that two words in the free band are equal if (and only if) they have the same initial and terminal marks, and their initials and terminals are equal in the free band themselves. This means that to check if two words are equal, we have to do some work checking that their initials and terminals are: but this is slightly easier, since for a word with $4$ different types of letters, say, the initial and terminal of this word have only $3$ different kinds of letters (as above, where the initial of $adcadbc$ is $adcad$, using only the three letters $a, d, c$). So we’re reducing the problem down to several sub-problems that are easier to solve, since less letters are involved. If we are struggling to check whether the initials/terminals are equal, then we can use this same technique again and check the initials of the initials, the terminals of the initials, and so on; all of these will have one letter less again. Let’s try an example now to see how this works.
Above, we calculated the initial, terminal, and initial and terminal marks of $adcadbc$. To avoid writing out these words all the time, some works use the following notation to show what the four components are:
\begin{align*}
adcadbc &\sim (\text{initial}, \text{initial mark}, \text{terminal mark}, \text{terminal})\\
&\sim (adcad, b, a, dbc)
\end{align*}
This is just a quicker way of writing out everything we need to know. Let’s now check whether that word, $adcadbc$, is equal to some other word, which we will pick to be $adcacadbadbc$. Have a quick think to see if you can spot an obvious sequence leading from one to the other; I can’t see one, so I’ll use the technique above. We can verify that:
$$adcacadbadbc \sim (adcacad, b, a, dbc).$$
We notice that the last three elements in the parentheses are equal to the ones calculated for the first word, so whether the two words are equal hinges on whether the first elements in the parentheses are equal: so is $adcad=adcacad$ in the free band? We could check this either by calculating the initials, terminals, and their marks for these two words, or we could notice that the $caca$ chunk in the second word is a duplicate which cancels down to $ca$, giving the first word directly. So indeed $adcadbc = adcacadbadbc$ in the free band.
We could also use the Green and Rees technique to verify, as proved earlier with the long sequence, that $abcacba = abcba$.
For long words on a large alphabet, however, this technique is quite slow. We can’t always spot nice cancellation like we could in the example above, so we can very well imagine a situation where we’re checking equality for two words using the letters $a,b,c,d,e,f$. With six letters, our initials and terminals we have to compare have five letters, which is still hard to do. To check whether the initials are equal, we will have to apply the technique again, breaking down the initials into initials and terminals with four letters. We might have to do the same with the terminals, so this gives us four equalities to check with words using $4$ different letters. It gets worse, because $4$ is still complicated, so each of these four equalities breaks down into two equalities with $3$ letters, giving $8$ checks total. This is a lot, and it gets worse as the alphabet size increases. For words using $10$ different letters, we can expect to be checking around $1000$ small equalities.
In 2010, Jakub Radoszewski and Wojciech Rytter found a faster method for checking whether two words are equal in the free band, which doesn’t get quite so inefficient for large alphabets. (Formally, we call this new method a linear time algorithm, which beats the exponential time algorithm I was describing by a long shot). Though it is difficult to explain and do by hand, computers can carry it out very efficiently. So, part of my work this summer alongside Murray and Reinis was to implement this faster method in the GAP Semigroups package. Yet to be incorporated as I write this post, our work currently lives here, and Reinis is still working to improve other aspects of GAP’s handling of free bands.
For question 4, somehow a lot of mathematicians are satisfied with using the method derived from Green and Rees to check whether words are equal in the free band—they don’t need to know that the exact sequence of steps is. However, finding an efficient algorithm remains an interesting question, and one that future students of Prof. Mitchell’s might be asked to work on. Until then, I plan to write some inefficient code to find sequences at some point, so that may appear on my GitHub. And who knows: if you’ve enjoyed this blog post enough, you might just be willing to tackle that problem too. Good luck!
References – Further Reading
Green, J. and Rees, D., 1952. On semi-groups in which x^r = x. Mathematical Proceedings of the Cambridge Philosophical Society, 48(1), pp.35-40.
Howie, J., 1995. Fundamentals Of Semigroup Theory, London Mathematical Monographs. Oxford: Oxford University Press. (Note: namely section 4.5)
Lothaire, M., 2005. Applied Combinatorics On Words. Cambridge, UK: Cambridge University Press. (Note: namely chapter 2)
Radoszewski, J. and Rytter, W., 2010. Efficient Testing of Equivalence of Words in a Free Idempotent Semigroup. SOFSEM 2010: Theory and Practice of Computer Science, pp.663-671.
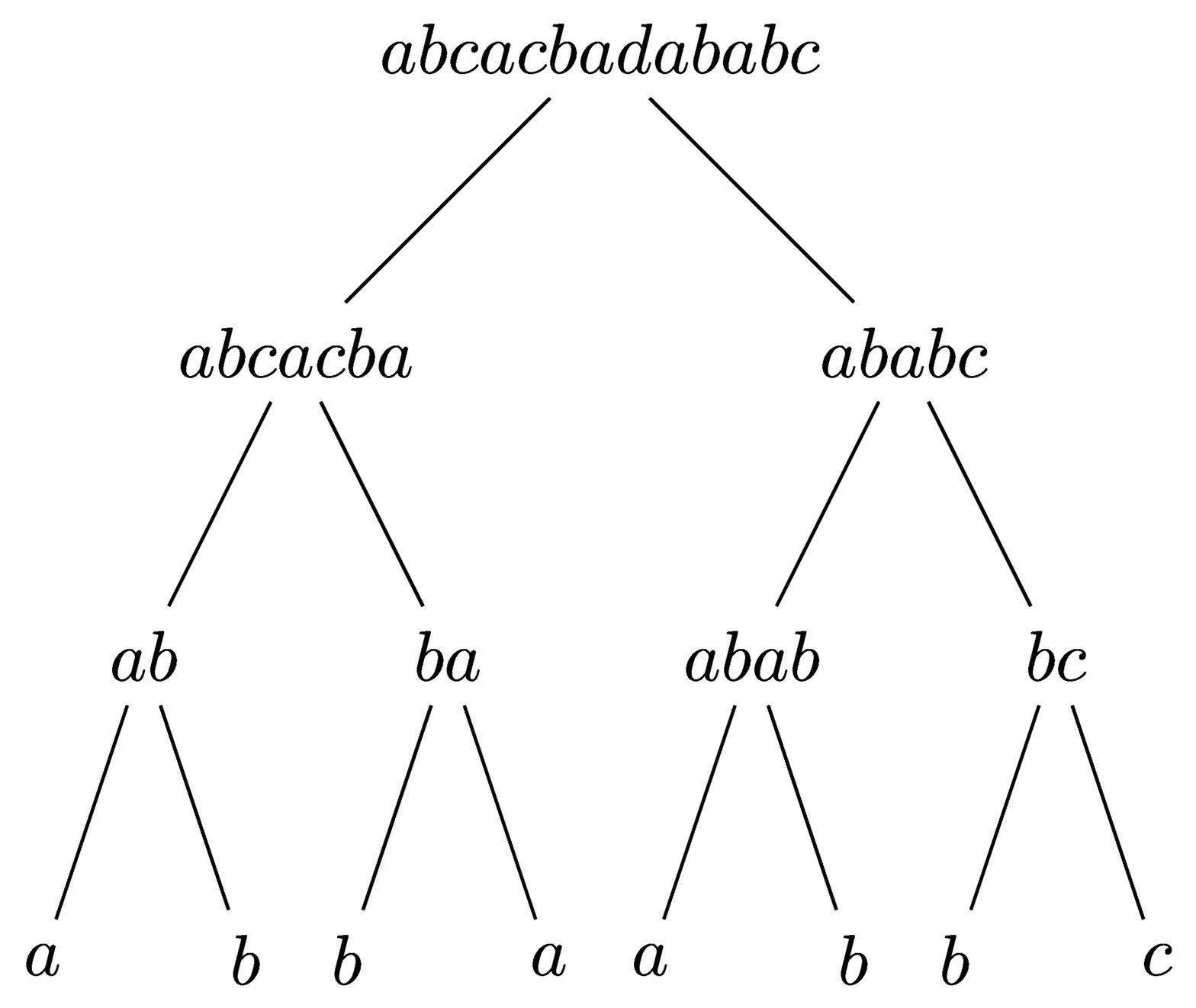
Here’s a solution that only uses 10 transformations
(AB)CACBA
ABABCA(CB)A
A(BABC)ACBCBA
AB[AB]CBABCACBCBA
ABCBABCAC(BCBA)
ABCBABCACB[CB]ABCBA
AB(CBA)BCACBABCBA
ABCBACBABC[ACBABC]BA
ABCBA[CBA]BCBA
ABCBA[BCBA]
ABCBA
Very nicely done!